Por qué deberías hacer una prueba A/B

¡Genial! ¡Así que el nuevo cambio que acabas de introducir en tu página de destino funciona mejor! Bueno, al menos eso es lo que parece, porque estás recibiendo más clics que la semana pasada, o tal vez ves que más usuarios llegan a tu página de pago y gastan más dinero en ella. Pero, ¿estás seguro de que es mejor que la última versión? Es posible que las métricas que te interesan estén funcionando mejor por ahora, pero ¿cómo sabemos si este éxito se debe a que se trata de una mejora real y no a un evento estacional (por ejemplo, cerca del día de pago o Navidad)? ¿Y qué pasa si, unas semanas más tarde, su rendimiento empieza a empeorar? ¿Simplemente volvemos a la primera versión?

Este problema no es infrecuente cuando se implementa Modelos de aprendizaje automático también. Probablemente iterará e implementará nuevas versiones de su modelo muchas veces, cambiando constantemente sus resultados. Por ejemplo, si ha logrado un gran avance en su sistema de recomendaciones, puede resultar tentador simplemente implementar el nuevo modelo directamente y usar este nuevo algoritmo para decidir qué recomendaciones recibirán TODOS los usuarios. ¡Pero qué pasa si realmente funciona peor que la versión anterior! Puede suceder que a los usuarios simplemente les gusten más las recomendaciones anteriores.

¿Qué es una prueba A/B?

Aquí es donde Pruebas A/B entra. Un Prueba A/B es una herramienta estadística que compara dos variantes, UN y B (¡de ahí su nombre!) por lo general se conoce como Controlar y Tratamiento (el que empezaste y el que quieres probar). El Tratamiento debería introducir el cambio que quieres probar, y una parte de tus usuarios debería estar expuesta a él, mientras que el resto debería seguir exponiéndose a Controlar. Después de cierto tiempo, la prueba A/B nos dirá qué tan seguros estamos de que una variante es mejor que la otra.

Esta idea se usa en todas partes hoy en día, ya sea para saber qué tan significativo es estadísticamente un experimento científico o para comprender el compromiso y la satisfacción de los usuarios de una aplicación o sitio web. Hay muchas cosas que debe saber para llevar a cabo este experimento y, lo que es más importante, para comprender correctamente y hacer una interpretación correcta de sus resultados.

En esta entrada queremos darte los fundamentos para implementar y entender tu propia prueba A/B y darte consejos para evitar caer en los muchos errores habituales que pueden ocurrir al ejecutar e interpretar tus experimentos. Hablaremos de Pruebas A/B usando un frecuentista enfoque, que es el marco más común. Es bastante simple de implementar, pero sus resultados pueden ser un poco difíciles de entender.

Primeros pasos

Hay algunas cosas que hacer antes de que podamos empezar a ejecutar un Prueba A/B:

• Defina su métrica objetivo y obtenga sus datos

Un Prueba A/B es un basado en datos proceso. ¡No puedes ejecutar tu experimento si no tienes datos sobre cómo responden los usuarios a tu aplicación! Esto va de la mano con la métrica con la que quieres experimentar: ¿te interesa mejorar la tasa de clics de una página determinada o quizás te preocupa que más usuarios lleguen a tu página de pago después de haberles ofrecido alguna oferta especial? Lo importante aquí es que te decidas por una sola métrica, y esta métrica debe ser clave para tu negocio. Piensa también en tu unidad de análisis: ¿son los usuarios, las sesiones, las cookies, los días o qué exactamente? Deberías poder extraer datos a nivel de esta unidad para la métrica que desees.

• Cree su variante de tratamiento y divida a sus usuarios

Después de saber con qué experimentar, puedes crear tu variante de tratamiento. Tal vez se trate de una página de destino nueva y elegante o de una nueva función de la que no estás del todo seguro de si será un éxito entre tus usuarios. Lo importante es que sepas qué usuarios cayeron en Controlar y Tratamiento variante, y que sigan viendo constantemente la variante asignada durante el experimento.

El hash es la forma de realizar esta tarea. Una buena regla general es combinar el nombre del experimento con la identificación de usuario y el hash mediante una función de hash estándar como MD5. A continuación, puede obtener el módulo del hash resultante para dividir a los usuarios. ¿Quieres una división 50/50? Solo tienes que asignar a una variante los usuarios con el último dígito de su hash terminado en 0-4 y los que terminan en 5-9 a la otra. ¿Quieres asignar solo el 10% de tus usuarios a cada variante? Lo mismo ocurre si ejecutas una operación de módulo, los usuarios cuyo hash termine en 00-09 deberían obtener una variante y los usuarios cuyo hash termine en 10-19 la otra.

• Defina su hipótesis y el tamaño de la muestra

Definir una hipótesis puede ser la parte más difícil a la hora de diseñar el experimento. Una vez que sepas qué métrica quieres usar para tu experimento y cuál utilizarás como variante, tienes que hacer una idea concreta hipótesis. Debido a su cambio, ¿cuál es el comportamiento de los usuarios que espera cambiar? ¿Y cuánto espera que afecte a su métrica clave?

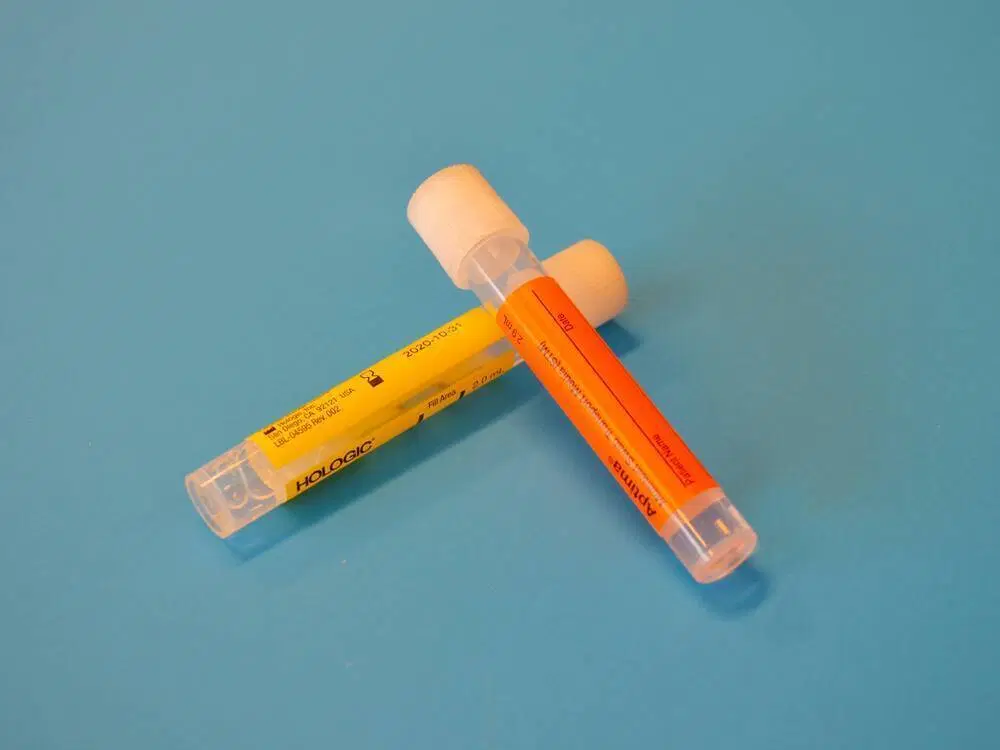
Saber esto nos permite definir el tamaño de nuestra muestra usando un calculadora sencilla. Por ejemplo, supongamos que queremos medir la tasa de clics de un botón de pago y ya sabemos que tiene una tasa de clics del 20%. Si queremos detectar un efecto de al menos el 5% en relación con la tasa de clics actual, necesitaríamos que participaran en el experimento 25 255 usuarios por variante. Más información sobre cómo usar esta calculadora y sus parámetros, por ejemplo valor p y poder estadístico ¡más tarde!

• ¡Conoce tu hipótesis nula!

Ejecutarás tu experimento en un hipótesis nula, que es lo que querrás descartar o no descartar. Ya tienes tu hipótesis para lo que esperas de tu Prueba A/B, pero el hipótesis nula está estrechamente ligado a la implementación de su prueba. Por ejemplo, el prueba t puede probar el hipótesis nula que las medias de dos poblaciones de muestra son iguales.

Para dar un ejemplo concreto, supongamos que ha estado haciendo un experimento con el tasa de clics de un botón de pago y ha alcanzado el tamaño de muestra necesario para obtener la respuesta a su Prueba A/B. Después de comprobar la tasa de clics, verá que Controlar la variante tiene una tasa del 3%, mientras que Tratamiento tiene una tasa del 5%. ¡Afortunadamente, la tasa de clics es la media de los usuarios que hicieron clic en el botón! Una opción perfecta para ejecutar un prueba t. A partir de sus resultados, podrás saber si sus medias son estadísticamente diferentes y si una es mejor que la otra, pero primero tendrás que aprender a entender sus resultados.

Comprensión de los resultados

Ahora que sabemos lo que necesitamos para iniciar nuestro Prueba A/B, es hora de que analicemos cuáles son sus resultados. Antes, cuando definíamos el tamaño de nuestra muestra con la calculadora, también podíamos haber elegido el deseado valor p y poder estadístico del experimento. Estos son conceptos clave para entender a un frecuentista Prueba A/B.

• valor p

Después de entender nuestro hipótesis nula, queremos estar seguros de cómo confiado estamos en estos resultados. En pocas palabras, un valor p es la probabilidad de que después de ver nuestras muestras, hipótesis nula es cierto. Un subidón valor p significa que es probable que sus datos sigan el hipótesis nula, mientras que un valor bajo significa que es poco probable que las observaciones lo sigan.

Por ejemplo, para prueba t mencionado anteriormente, si lo ejecutamos y obtenemos un valor p podemos evaluar que es posible que no haya diferencia entre las medias de las muestras, mientras que un valor bajo significa que tenemos pruebas suficientes para rechazar esta hipótesis, lo que nos permite confirmar que las medias de las muestras son lo suficientemente diferentes. Un umbral que se utiliza habitualmente para confirmar si los resultados son estadísticamente significativo es $0.05\ %$, lo que significa que hay una probabilidad de $5\ %$ de que hipótesis nula siendo correcto (y sus resultados son fortuitos).

• Poder estadístico

El fuerza de tu experimento, la probabilidad de no rechazando la hipótesis nula cuando en realidad había suficiente diferencia en las muestras como para descartarla. Una más alta Potencia significa una menor probabilidad de cometer este error (¡pero significa que necesitará más muestras para asegurarse de que esto suceda!). Un valor común para el poder estadístico es $80\ %$, o si lo vemos al revés, que está de acuerdo con no rechazar la hipótesis nula los $20\ %$ de las veces.

Poniéndolo todo junto

Ahora, usemos todo lo que hemos aprendido para ejecutar nuestro propio experimento: queremos implementar un sistema de recomendación de artículos de noticias basado en Aprendizaje profundo para competir contra nuestra implementación anterior usando Factorización matricial y comprueba si hay más usuarios haciendo clic en las recomendaciones que se muestran. Ya conocemos nuestro antiguo Factorización matricial el sistema de recomendación tiene una tasa de clics del 20%. Vamos a trabajar el experimento paso a paso.

• Definir la métrica objetivo: ya que queremos ver si más usuarios hacen clic en lo que recomendamos, podemos utilizar una tasa de clics (de ahora en adelante CTR) como nuestra métrica objetivo.

$$CTR =\ frac {\ text {Cantidad de usuarios que hicieron clic en una recomendación}} {\ text {Cantidad de todos los usuarios a los que se les mostró una recomendación}} $$

• Obtenga los datos necesarios: sin datos no podremos ejecutar el experimento. Tendremos que almacenar todos los eventos de los usuarios en nuestro sitio web y poder diferenciar entre cada usuario individual y saber si ha estado expuesto a la Controlar o Tratamiento variación.

Digamos que terminamos con un marco de datos que se ve así:

Variante de clic de fecha 2020-06-170 Control 2020-06-170 Tratamiento 2020-06-170 Control 2020-06-171 Tratamiento

• Definir una hipótesis: nuestra hipótesis será que nuestro nuevo sistema de recomendaciones no es mejor en un cierto porcentaje. Al menos eso es lo que nos dice nuestro instinto después de probarlo por nosotros mismos. Sin embargo, seremos conservadores y esperamos que nuestro nuevo sistema funcione al menos un 10% mejor que el original.
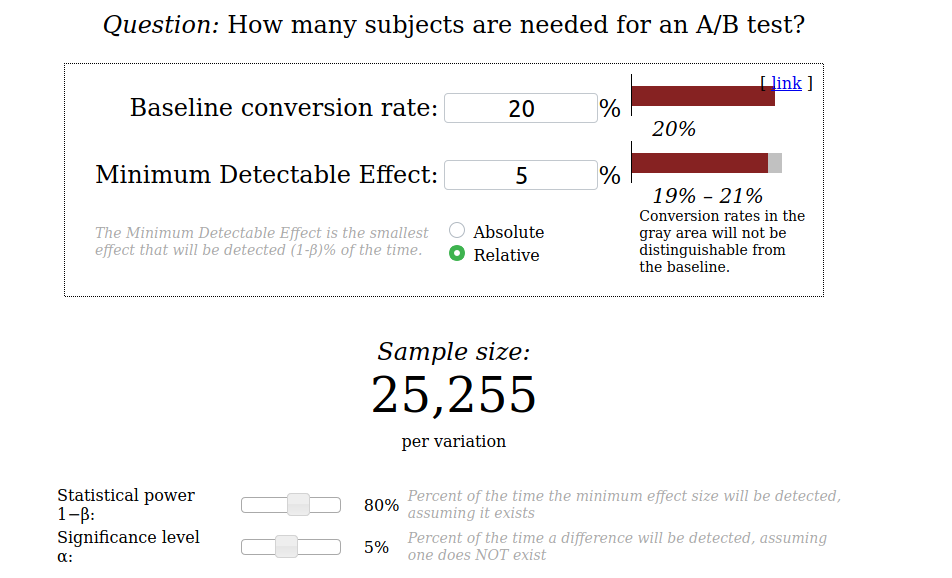
• Obtenga el tamaño de la muestra con la calculadora: ejecutaremos lo mismo calculadora con nuestros valores: a tasa de conversión de referencia del 20% y Efecto mínimo detectable del 10%. Usaremos el umbral clásico del 5% para valor p y un 80% para el poder estadístico.

• Conoce nuestra hipótesis nula y prueba: en este caso el prueba t se ajusta perfectamente, ya que queremos comparar las medias de nuestras muestras (las CTR en este caso). Usaremos escipiaes implementación de la prueba t, y veamos si podemos rechazar la hipótesis nula.
• Ejecute el experimento: ¡esta es realmente la parte fácil! Tras realizar el experimento durante una semana, obtenemos incluso más muestras de las necesarias, lo que nos permite comprobar los resultados con confianza. Dividamos las Controlar y Tratamiento da como resultado su propia matriz y ejecuta el prueba t:

fromscipy.statsimportttest_indcontrol=df [df ['variant'] =='Control'] treatment=df [df ['variant'] =='Treatment'] statistic, pvalue=ttest_ind (control ['click'], treatment ['click']) print (F'p-value: {pvalue} ') print (F' ¿El valor p es menor que el umbral? {pvalue<0.05} ')

• Comprenda los resultados: ejecutando el código anterior recibimos la buena noticia de que nuestro valor p ¡es más pequeño que el umbral!

Valor p: 1.0883040680514908E-66 ¿El valor p es menor que el umbral? ¿Cierto

Al entrar en los datos, podemos ver que Tratamiento tiene una tasa de conversión del 40%. Con esto, podemos decir con seguridad que nuestra nueva implementación está funcionando, como mínimo, 10\ %$ mejor.

Los pecados de las pruebas A/B

Como puede ver, ejecutar un Prueba A/B frecuentista no es difícil, pero tiene muchas partes móviles que necesita conocer para comprender correctamente sus requisitos y resultados. Se pueden cometer muchos errores al ejecutar Pruebas A/B!

• No implemente código mientras se ejecuta

La implementación de código que realiza grandes cambios significa que su experimento es sobre. Si lo mantienes en funcionamiento, ¡estarías experimentando con dos implementaciones completas de una variante! Nunca sabrás si tu nueva variante está funcionando mejor o peor por la forma en que estaba antes o después de la implementación. Por supuesto, hacer correcciones rápidas está bien, siempre que sean pequeñas y ambas variantes se hayan ejecutado correctamente (si una de ellas ha redirigido a los usuarios a una página de error, ¡empieza de nuevo!).

• Consecuencias de los hashes incorrectos

Anteriormente mencionamos lo importante que es una buena función de hash para dividir correctamente a nuestros usuarios. Pero, ¿qué pasaría si no la usáramos en absoluto? Digamos que solo usamos un módulo función, obteniendo los últimos dígitos de la identificación de usuario y usándolos para dividirlos en diferentes grupos. Pero, ¿qué pasa si esas distribuciones son desiguales y es más probable que un determinado tipo de usuario tenga un último dígito determinado? Y ten en cuenta que, cuando termine tu experimento, reutilizarás el mismo módulo ¡La función para un nuevo experimento dividiría a los usuarios de la misma manera! No queremos que eso suceda, ya que los resultados del último experimento afectarían al nuevo, y los usuarios podrían estar más o menos contentos según la última variación que hayan visto.

• ¡Sin echar un vistazo!

Montones de signos estadísticos se comprometen a la hora de averiguar la importancia de la prueba A/B. Por ejemplo, haciendo un parada temprana de su experimento (llamado problema de asomo) implica tomar una decisión antes de alcanzar el tamaño muestral requerido, deteniéndose el experimento antes de lo que se supone que debe terminar. Es un problema clásico que es el que más nos duele cuando estamos ansiosos por tomar una decisión sobre nuestro examen. Es tentador tomar decisiones antes de que termine el experimento (¡especialmente si nos gustan los resultados que estamos viendo!). No hay problema en monitorear y analizar el estado actual de nuestro experimento, pero debemos evitar tomar decisiones al respecto se asoma cueste lo que cueste. Realmente no es lo mismo echar un vistazo varias veces a nuestro valor p e intentamos tomar una decisión cada vez si nos gustan sus resultados que utilizar los resultados adquiridos después de alcanzar lo requerido punto de parada (aquí y aquí ¡son excelentes fuentes sobre este tema!).

Alternativas

Hemos mencionado muchas características de pruebas frecuentistas que son un poco molestos: no nos permite detener el experimento antes de tiempo y entender cosas como la valor p ¡no es fácil! Además, siguiendo nuestro ejemplo, trabajamos esperando ver grandes cambios con nuestro Tratamiento variante. Después de cierto punto, tus experimentos probablemente consistirán en conseguir un pequeño (pero importante) aumento de tu métrica clave. Y cuanto menor sea el cambio esperado, ¡mayor será el tamaño de la muestra necesario para detectarlo!

¿Qué pasa si queremos obtener inferencias correctas de nuestro experimento sin necesidad de obtener todas nuestras muestras, o qué pasa si queremos detenerlo de forma segura y temprana porque realmente estamos viendo un buen o mal rendimiento?

¿Qué podemos hacer para abordar estos problemas de las pruebas A/B? Por suerte, podemos usar algunos enfoques alternativos para nuestros experimentos:

• Pruebas A/B secuenciales frecuentistas: aborda la problema de asomo y permite varios «puntos de control», donde podemos detener nuestro experimento de forma segura en lugar de hacerlo antes de lo previsto.
• Pruebas A/B bayesianas: resuelve el problema de asomo permitiéndote ver el experimento en cualquier momento y aun así hacer inferencias perfectas y válidas a partir de él.

Discurso de clausura

Como puede ver, hay muchas partes móviles que entender en un Prueba A/B. Es frecuentista La versión es fácil de implementar, pero bastante difícil de entender. Por eso es importante comprender sus fundamentos y asegurarse siempre de aprender de las personas que han caído en las partes más turbias de Pruebas A/B ¡y salió vivo!

Hay muchos temas para seguir ampliando nuestra A/B conocimiento, como experimentar con No binomial las métricas y las alternativas a frecuentista pruebas mencionadas anteriormente. ¡Estén atentos a las próximas entradas sobre estos temas y más!

Referencias

Miller, Evan. «Calculadora de tamaño de muestra». Las increíbles herramientas A/B de Evan, URL

Miller, Evan. «Cómo no ejecutar una prueba A/B». Evan Miller, 18 de abril de 201, URL

Trencseni, Martín. «Hermosas pruebas A/B». Peón de bytes, 05 de junio de 2016, URL

Mullin, Shanelle. «La guía completa para las pruebas A/B: consejos de expertos de Google, HubSpot y más». Shopify, 10 de abril de 2020, URL

Draper, Paul. «El defecto fatal de las pruebas A/B: echar un vistazo». Gráfico Lucidchart, URL

Las imágenes de esta entrada pertenecen a Historia de la ciencia de Wikimedia Commons:

Montgolfier: Cyrille Largillier/CC BY-SA (https://creativecommons.org/licenses/by-sa/4.0).

El alquimista: Carl Spitzweg/Dominio público.